Background:
35 y/o male. Previously very healthy. Competitive endurance athlete (Ran a 2:46 marathon in 2024). For reference, normal resting heart rate was in the low 40’s bpm. “Easy” running pace (HR < 130 bpm) was ~8:00min/mi.
- Contracted EBV in November 2024. Acute infectious mononucleosis (fever, sore throat) lasted ~2weeks. Confirmed first-time infection via EBV antibody panel. (Not a reactivation)
- Fatigue persisted through January – February 2025, but other than not being able to train, lived essentially normal life. (40+ hour work week, family and social activities, gardening, etc.) Went on a few easy jogs 9:00 min/mi, HR 130-140. No issue recovering and performing daily activities post run. But could tell I was not back to 100% and did not want to push it.
- Fatigue worsened in March. Continued to work and perform family/social activities. No running at all.
- On 3/31/25 had EBV antibodies re-tested. Showed elevated IgM, IgG, EBNA, EA-D. (IgM should have disappeared by this point).
- Deteriorated further in April. Hospitalization after waking with full body tremors one night.
- Continued decline throughout May and June. Have seen multiple specialists to no avail. Seems like I may be rapidly progressing to developing full blown ME/CFS.
Current Symptoms:
- Elevated resting HR (compared to my baseline) – now consistently in low 50’s while sleeping; 60’s laying supine awake; 70’s sitting upright — This confuses doctors because they see these numbers as “normal.”
- Tachycardia on minimal movement (110 bpm getting dressed)
- HR 170+ with 5min of light walk/jog – HR still 130 an hour later (no recovery) – heavy lactic acid build-up and DOMS. This is much more than would be expected due to just “de-conditioning” (as some uninformed doctors have wanted to suggest).
- Heart arrhythmias – developed since April.
- Fatigue that does not improve with rest.
- Post exertional malaise – sitting upright in a chair for several hours one day leaves me in bed the next day.
- Tremors, Night sweats, Heat Intolerance, numbness/tingling in hands & feet, burning sensation on skin (intermittent).
- Intermittent mild hypoxia (93-94 O2 sat) and air hunger.
- Abnormal lab values: Low WBC, High RDW%, Low MPV, Low BUN, High CO2 (repeated in multiple tests over the last 6 weeks) .. Misshapen RBC’s – “dacrocytes” noted on manual smear in June. (none were present in mid-April)
- EBV panel in mid-June still showed elevated IgM, IgG, EBNA, and EA-D. Started taking Valacyclovir 1g x 3/day.
What you have written about ME/CFS and coagulation makes a lot of sense with what I am experiencing. My Thorne microbiome test appears to present lots of opportunity for improvement as well…
I look forward to your insights and analysis.
Thank you for your time and consideration of my case,
Given EBV Involvement …
My wife had EBV and EBV-Specific Transfer Factor was highly effective for her. The problem is that it appears to be no longer available. This gives some background: Transfer Factor: Myths and Facts [2020]
- Treatment of childhood combined Epstein-Barr virus/cytomegalovirus infection with oral bovine transfer factor [1981]
- Specific transfer factor with activity against Epstein-Barr virus reduces late relapse in endemic Burkitt’s lymphoma [1990]
- Transfer factor with anti-EBV activity as an adjuvant therapy for nasopharyngeal carcinoma: a pilot study [1996]
- The use of transfer factors in chronic fatigue syndrome: prospects and problems [1996]
- Lessons from a pilot study of transfer factor in chronic fatigue syndrome [1996] ” Of the 20 patients in the placebo-controlled trial, improvement was observed in 12 patients, generally within 3-6 weeks of beginning treatment”
Immunization of donor animals: Animals are immunized with an EBV antigen, such as recombinant EBNA-1, a nuclear antigen of the Epstein-Barr virus. The antigen can be introduced via injection. The milk from the animal is then processed. [More Info]
There are Transfer Factor products on the market — but none appears to be EBV specific (which is what my wife used). It may be worth trying some of them — the apparent lack of specificity of these products is a concern. My memory is that the hosting animal is critical for its effectiveness. There are notes on it’s use on Hemex Protocol and Dave Berg, unfortunately the website selling the version they used is no longer there.
I did a quick search for chronic active EBV (CAEBV) treatment and nothing stands out as being very effective [more info]. It is an area of active research.
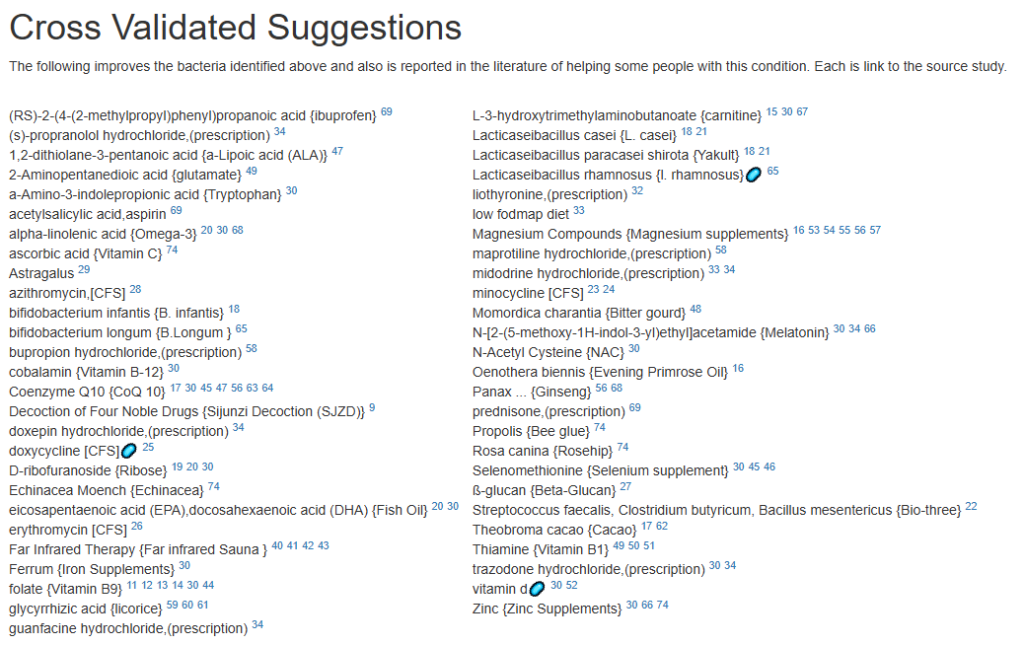
Trying to support the immune system to deal with CAEBV by Microbiome Manipulation
Premise: An infection (including virus) alters the microbiome to be optimal for it survival. Correcting the dysbiosis, weakens the infection (i.e. you may starve it of essential metabolites)
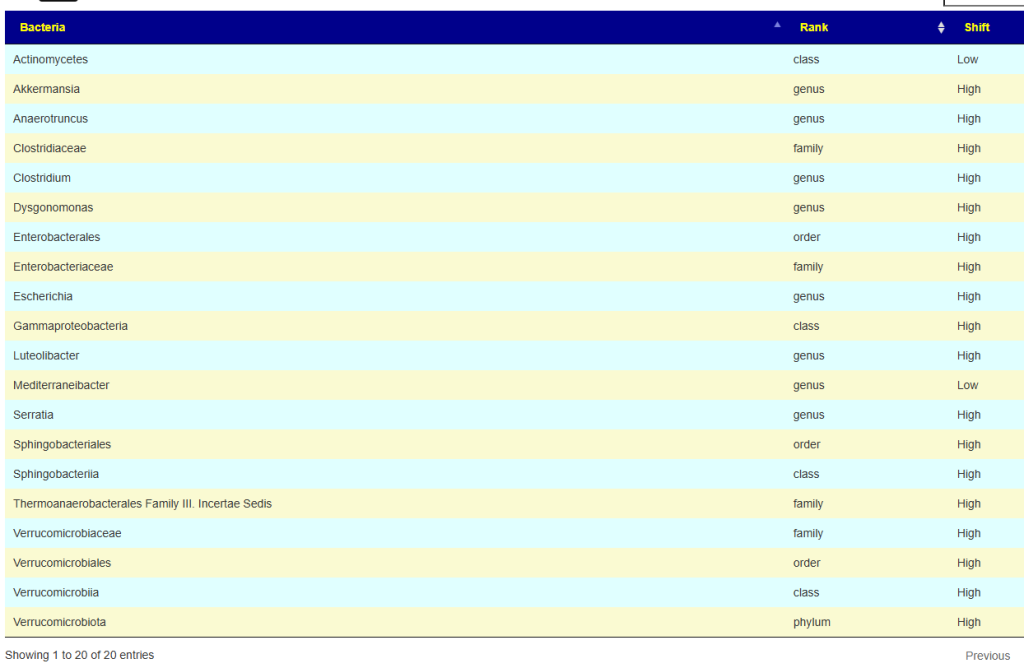
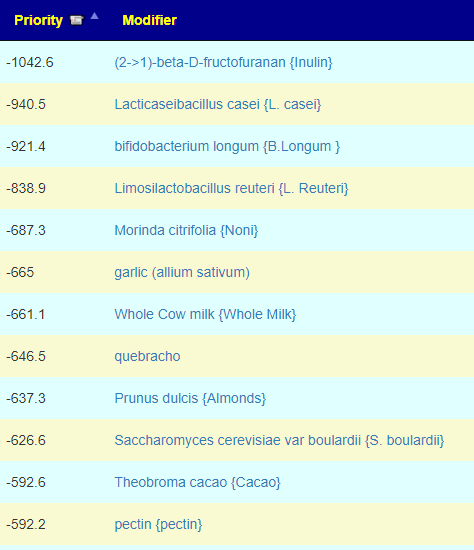
From other samples reporting EBV, we have many associations (different bacteria for different test unfortunately: Why this is expected). Thorne tests was not one of those that we had sufficient data (uBiome, Ombre/Thryve, Biomesight). Thorne also gives percentile ranking which opens a backdoor. I went into the data and found only 5 samples marked with EBV.
The following were found out of range consistent across these sample, all extremely low ( < 5%ile)
- Faecalibacterium genus
- Faecalibacterium prausnitzii species
- Eubacteriales order
- Clostridia class
To my delight, these collapses into one bacteria linerage: Bacillota; Clostridia; Eubacteriales; Oscillospiraceae; Faecalibacterium; Faecalibacterium prausnitzii
This makes suggestions very easy:
- Go to Faecalibacterium
- for linerage, you want the second from the left.
- The information included it’s children and its parents modifiers,
- i.e. Oscillospiraceae; Faecalibacterium; Faecalibacterium prausnitzii )
- Sort and filter the long list of items to increase it.
CAUTION: Faecalibacterium is not listed in the above EBV association page using other labs, nor is it reported in any published studies.
In terms of probiotics we have this list (based on number of studies reporting — not impact):
- Saccharomyces cerevisiae var boulardii {S. boulardii}
- bifidobacterium longum {B.Longum }
- lactobacillus acidophilus {L. acidophilus}
- Lacticaseibacillus casei {L. casei}
- Lacticaseibacillus paracasei {L.paracasei}
- Enterococcus faecium {E. faecium}
Fortunately a recent addition allows us better information, including relative impact! Going to Microbiome Taxa R2 Site, we see the probiotics ranked by impact that increases this bacteria:
- 40% Enterococcus faecium #1
- 34% Akkermansia muciniphila #2
- 30% Bacillus (mixture of different one) #3
- 19% Levilactobacillus brevis #X
- 14% Lactococcus lactis #X
- 14% Ligilactobacillus salivarius #X
- 10% Bifidobacterium catenulatum #X
This is the core set of probiotics to try. I would suggest 1-2 weeks of each and then rotate to the next one. After the third one, do one of the X for a week and then repeat.
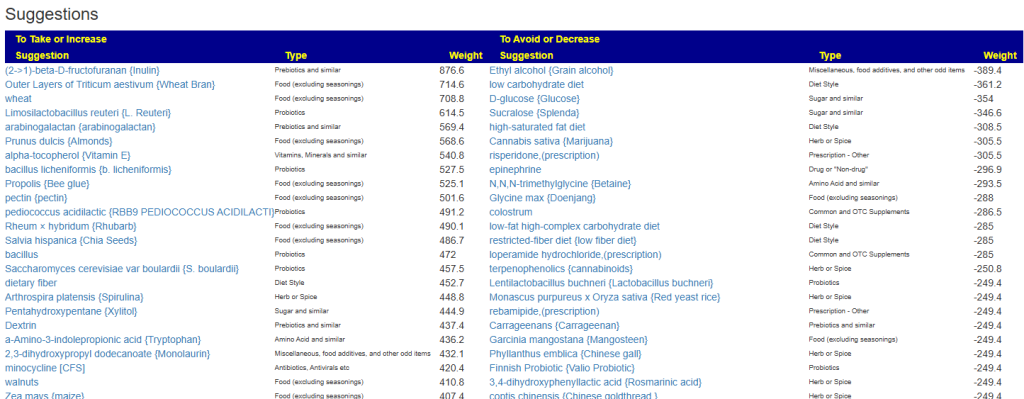
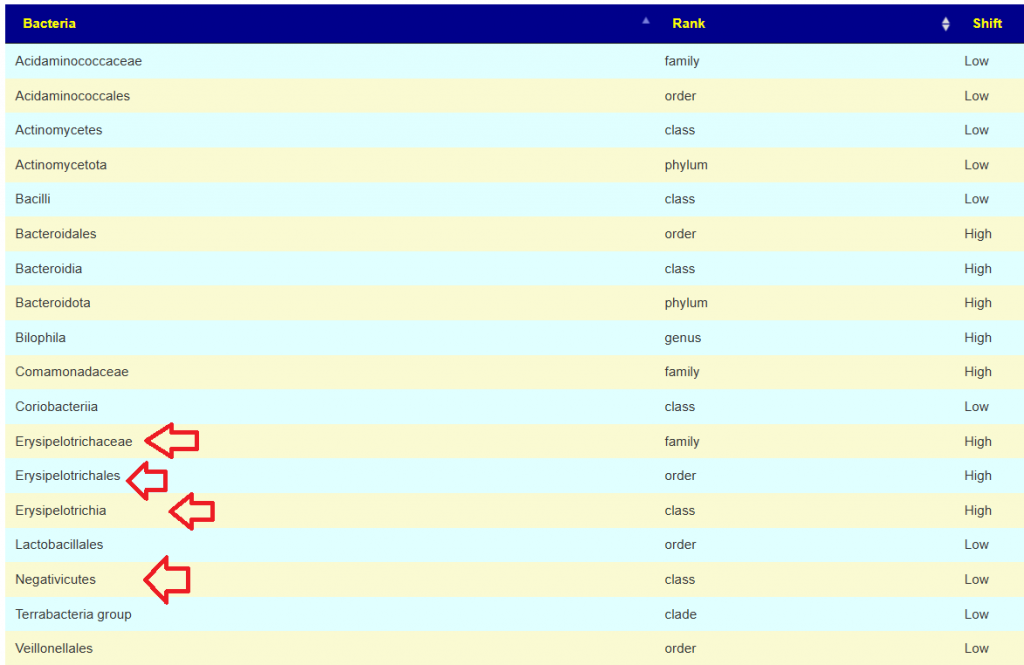
More relaxed patterns of 80% of samples showing consistent highs across 4 of the samples. There is a clustering around Corynebacterium, so we want to pick items to decrease it. As above, we should go to Corynebacterium
- Negativicoccus massiliensis species
- Peptoniphilaceae family
- Tissierellia class
- Corynebacteriaceae bacterium ‘ARUP UnID 227’ species
- Staphylococcus lugdunensis species
- Tissierellales order
- Corynebacterium simulans species
- Corynebacterium jeikeium species
- Corynebacteriaceae family
- Methylobacterium genus
- Corynebacterium singulare species
- Corynebacterium genus
- Corynebacterium striatum species
- Trichosporonaceae family
- Trichosporonales order
- Corynebacterium segmentosum species
- Methylobacteriaceae family
- Peptoniphilus harei species
- Anaerococcus genus
- Tremellomycetes class
- Staphylococcus genus
- Staphylococcaceae family
- Corynebacterium camporealensis species
And for lows:
- Bifidobacterium breve species
- Muribaculum genus
- Lachnospiraceae bacterium KM106-2 species
- Roseburia intestinalis species
- Blautia obeum species
- Pseudobutyrivibrio xylanivorans species
- Pseudobutyrivibrio genus
- Chitinophaga genus
- Coprococcus sp. ART55/1 species
- Lachnospiraceae bacterium species
This adds one more probiotic: Bifidobacterium breve which I would include in the #X rotation above.
EBV and Coagulation
Epstein-Barr virus (EBV) infection can be associated with significant coagulation abnormalities, particularly in the context of hemophagocytic lymphohistiocytosis (HLH) and EBV-associated lymphoproliferative disorders. [more info]
If practical, I would suggest the Hemex Panel which is a very complete test of the many vectors of coagulation. The other aspect is checking for genetic variations — often some are not clinically significant for a healthy person. When the immune system and/or microbiome is dysfunctional then they may “flare”. For myself, it was Prothrombin G20210A (Factor II Mutation) which may present itself as a cramp or Charley horse . I was lucky because selected supplements (piracetam and turmeric) was able to mitigate it.
There can be a problem because specialists may deem these issues to be “sub-clinical” (i.e. not worth intervention — i.e. not a stroke or visible Deep Vein Thrombosis). This same issue may be devastating for quality of life – physical or mental impairment.
For myself, I was reckless and took the highest daily dosage of aspirin for 10 days. The change that it caused convinced my MD that coagulation testing was warranted (perhaps to stop my reckless taking more aspirin!).
Back to addressing Microbiome Dysfunction …
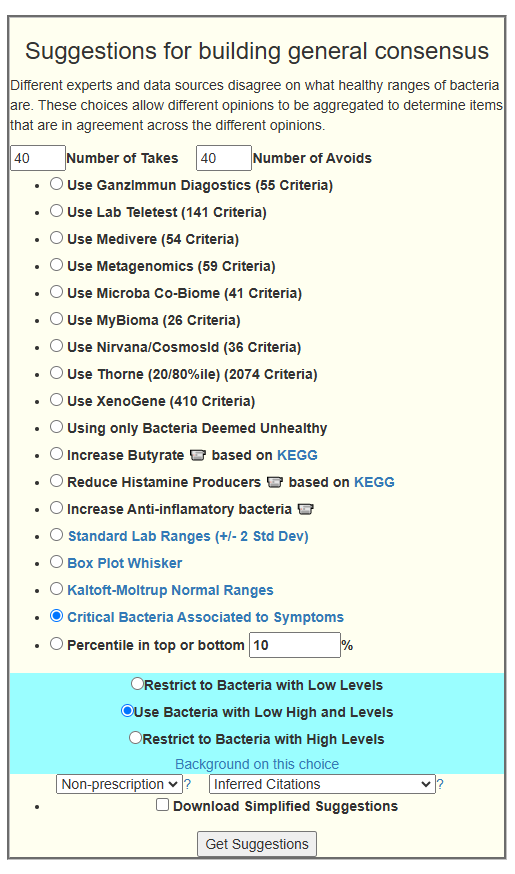
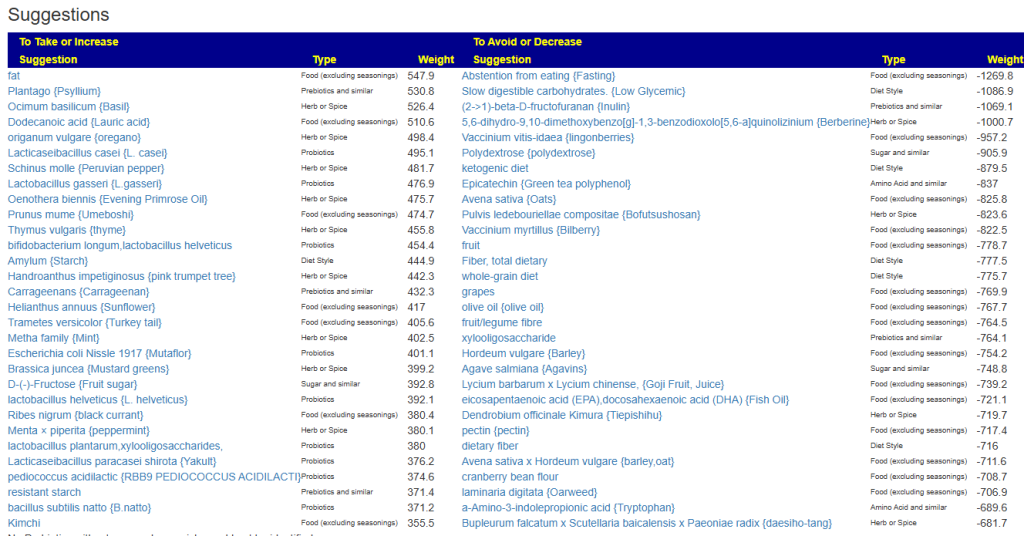
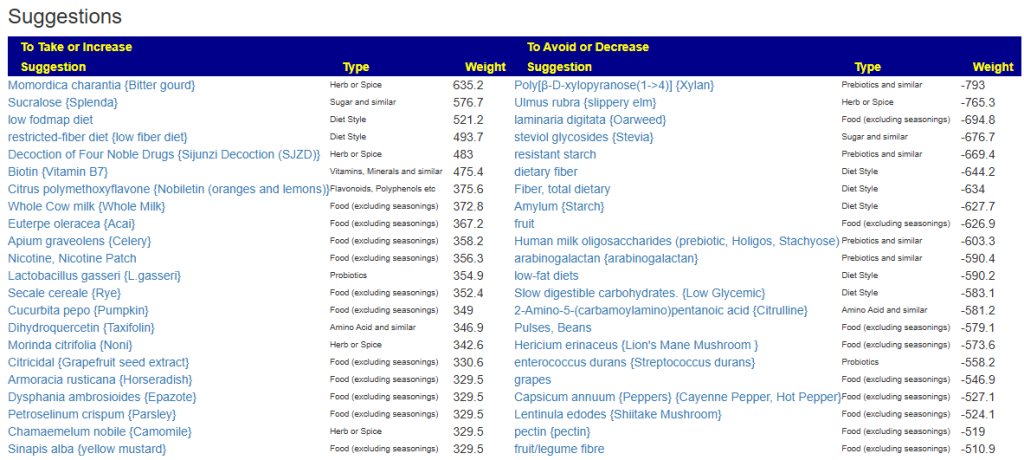
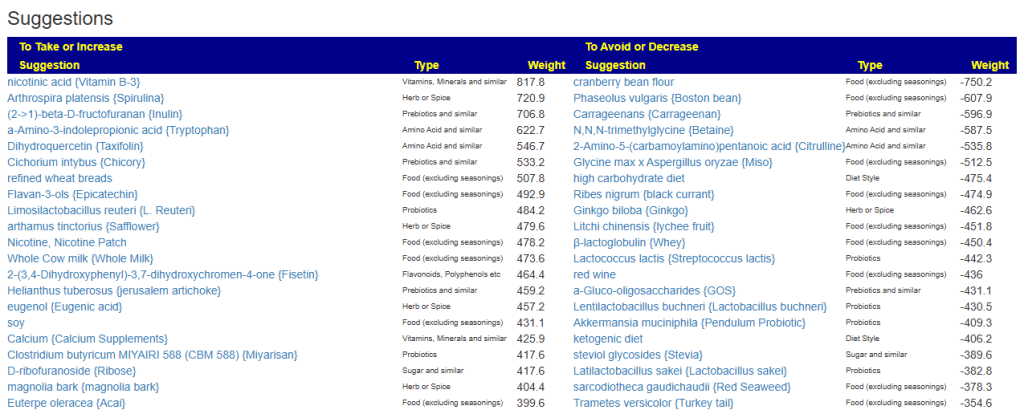
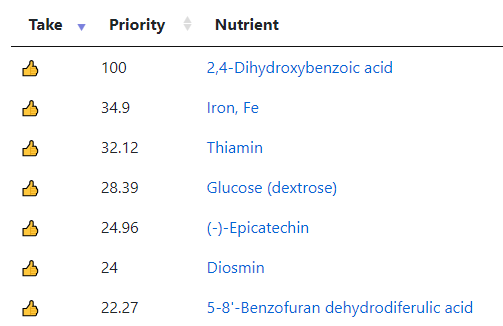
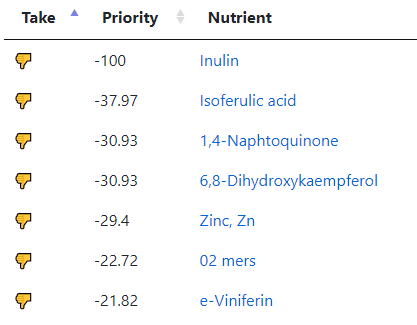
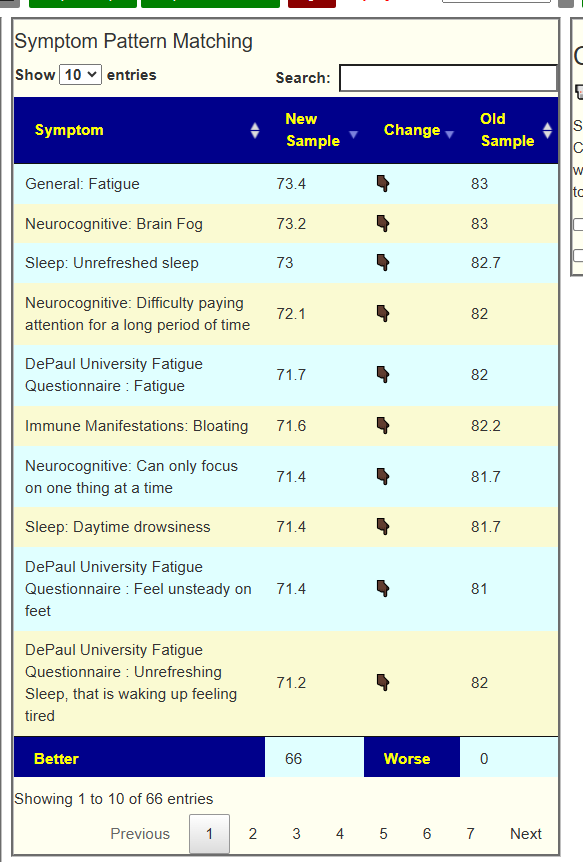
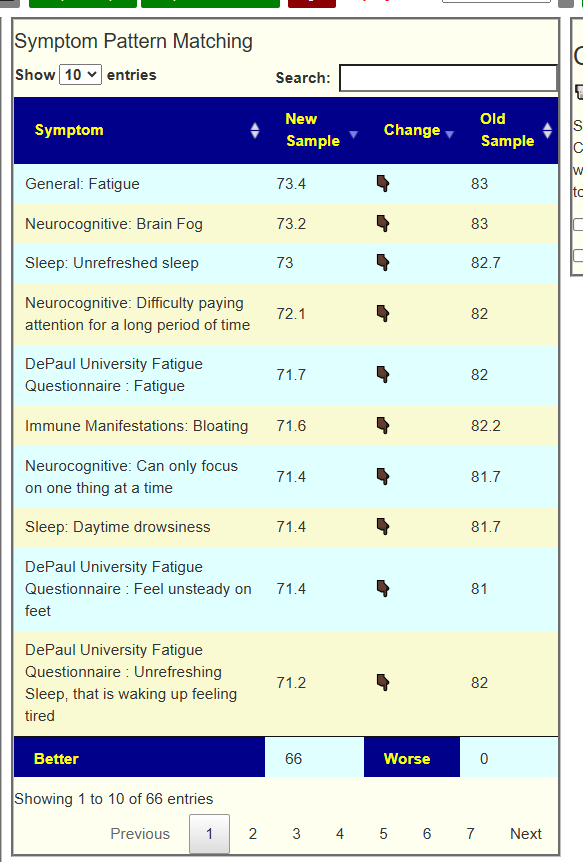
My preferred approach is to use Symptoms with statistical association based on the lab. This is not available for Thorne. In this case, my approach is to use the generic (that works off high and lows alone)
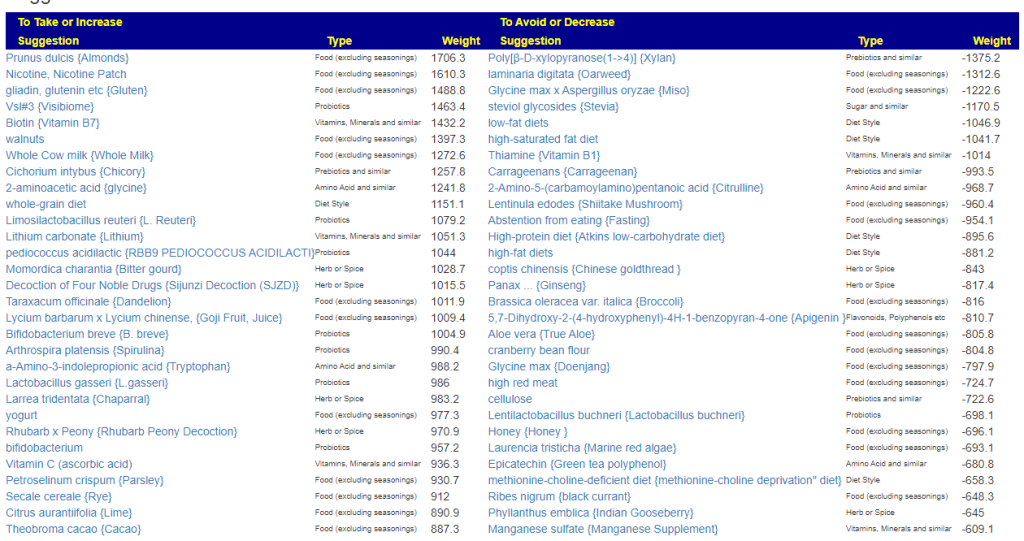
- Novice: Just tell me what to take or avoid
This gives 220 target bacteria. This is a high number, but given your back story — not shocking.
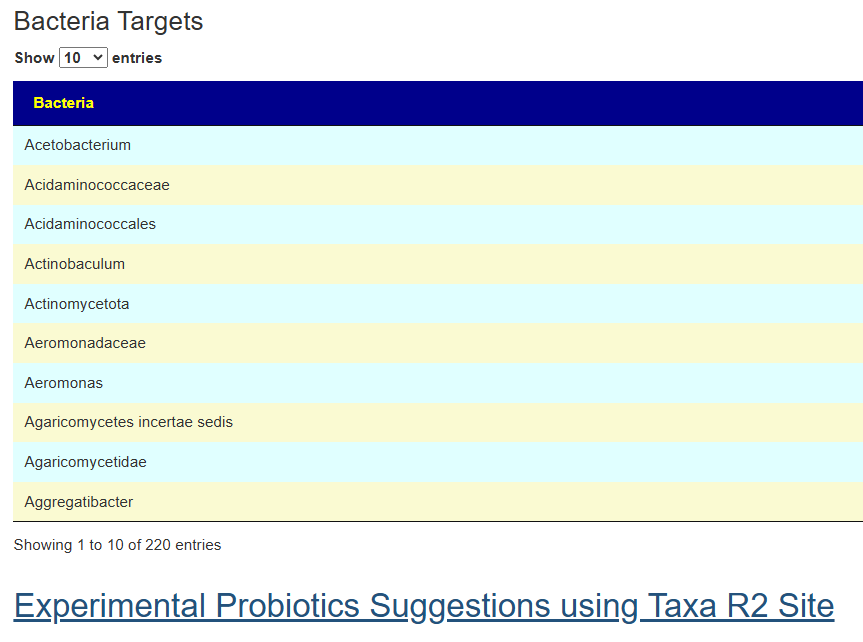
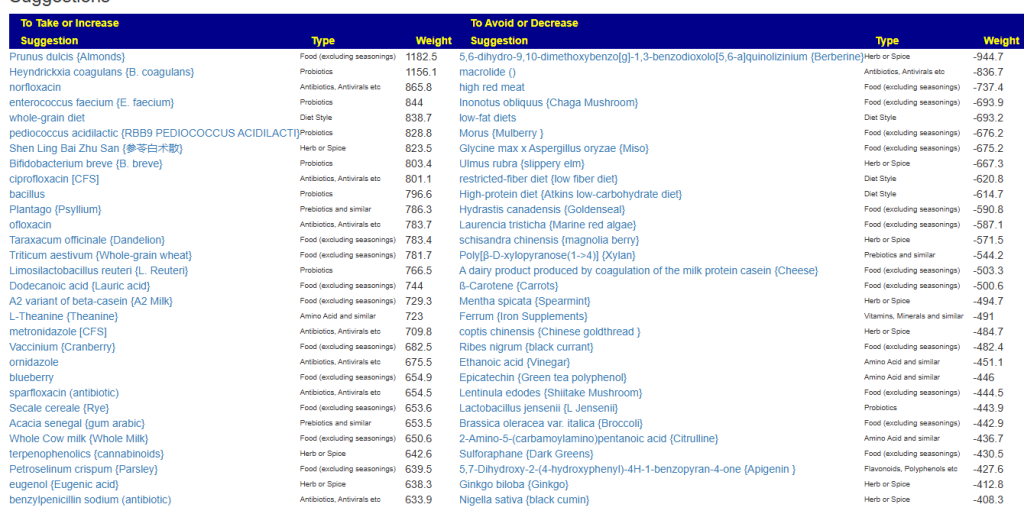
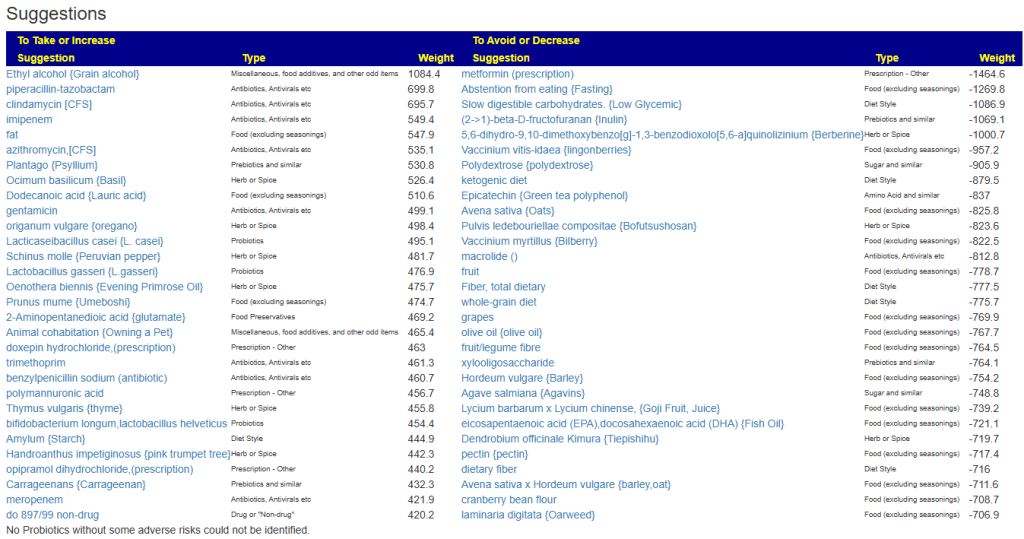
Clicking on the bottom link, takes us to the Microbiome Taxa R2 Site looking at all of these shifts. We get the following probiotics recommendations (with almost 2 dozens to avoid):
- 841 — Enterococcus faecium [EBV] —
- 676 — Lactococcus cremoris —
- 468 — Bifidobacterium adolescentis – 206
- 422 — Akkermansia muciniphila [EBV] – 265
- 350 — Lactococcus lactis [EBV] – 30
We have 60% of them matching the above list. At the end of each line, I included the Priority from the consensus (– not listed, likely because of no studies). Remember, no one knows the right way, I try different logical algorithms and look for items that everyone agrees on.
For completeness, let us look at the other items suggested:
- 190 — Bifidobacterium breve {B. breve} – 226
- 205 — Levilactobacillus brevis – 512
- 95 — Ligilactobacillus salivarius {L. salivarius} – 30
- 291 — Bifidobacterium catenulatum – 154
IMHO – We have probiotics nailed!
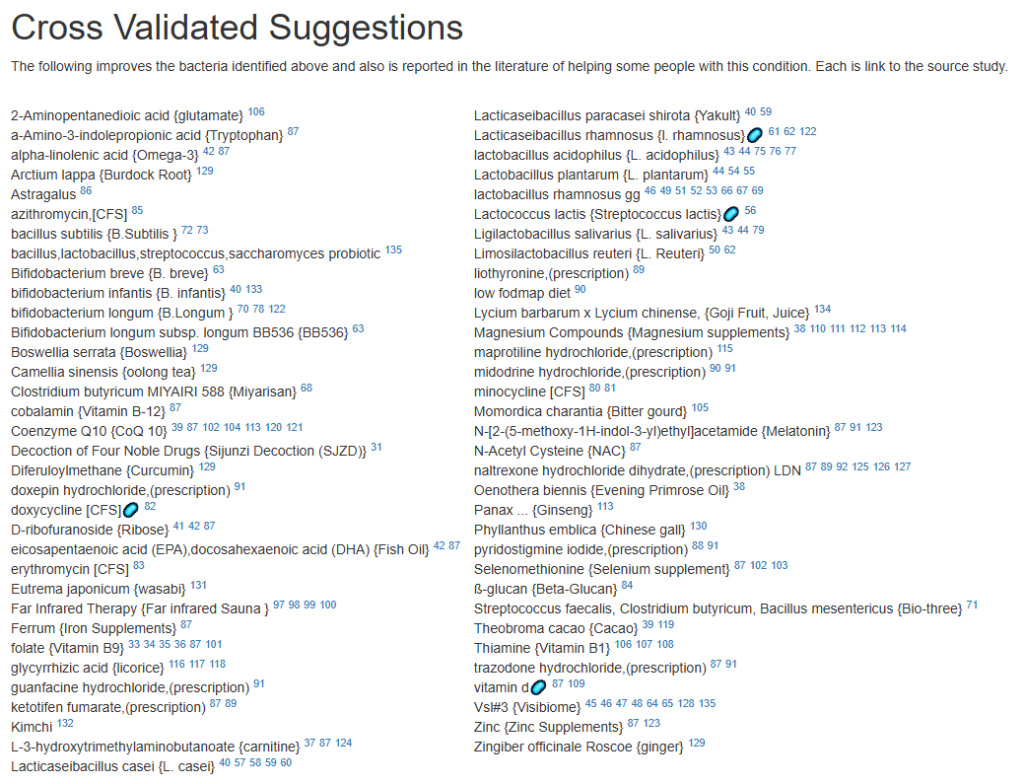
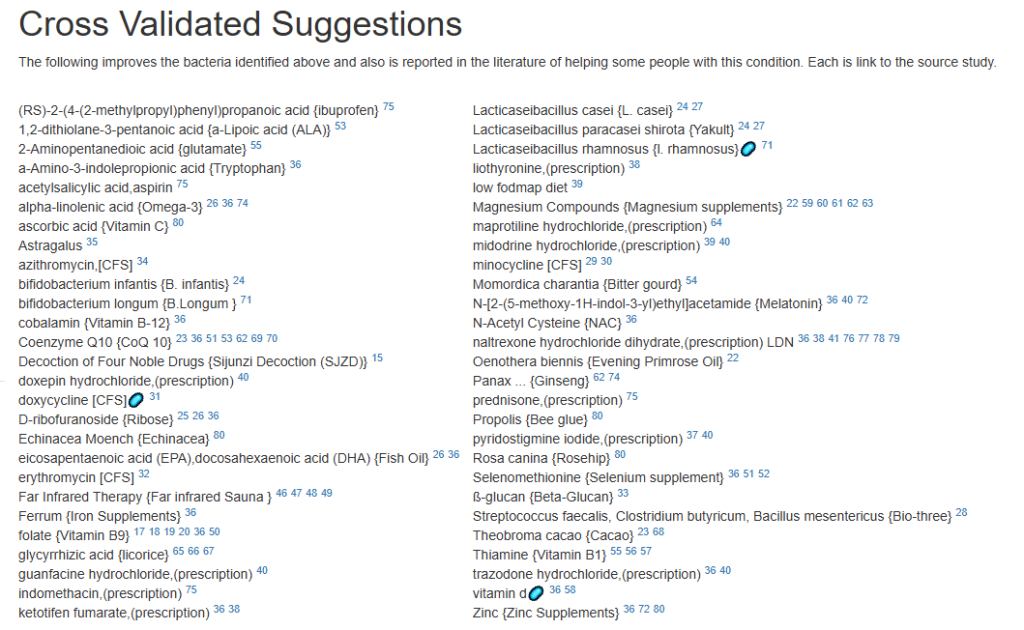
Let us look at other vectors from the consensus list. Order by priority. Emphasis should be on ones that are around 500 or higher (1/2 of highest priority)
- Vitamins, Minerals and similar (I must admit, I was surprise how many of these were EBV related)
- 642 Selenomethionine {Selenium supplement}
- Selenium deficiency is associated with increased susceptibility to EBV infection and its complications [more info]
- 512 nicotinic acid {Vitamin B-3}
- 453 Zinc {Zinc Supplements}
- Zinc is directly required for EBV gene regulation.[more info]
- 323 Silver nanoparticles {Colloidal silver}
- Inhibition of EBV replication: Silver nanoparticles stabilized in citrate buffer can inhibit EBV replication by up to 70% [more info]
- 301 Magnesium Compounds {Magnesium supplements}
- Magnesium plays a critical role in the immune response to Epstein-Barr Virus (EBV), particularly in individuals with genetic defects affecting magnesium transport: [more info]
- 291 Riboflavin {Vitamin B2}
- 275 alpha-tocopherol {Vitamin E}
- Vitamin E has demonstrated inhibitory effects on Epstein-Barr Virus (EBV) transformation of human B cells, particularly under conditions of oxidative stress: [more info]
- 642 Selenomethionine {Selenium supplement}
- Herb or Spice (top 3 only — very long list)
- 747 Olea europaea {Olive leaf}
- Olive leaf extract (OLE) has been shown in multiple studies to have significant antiviral and antioxidant activity against Epstein-Barr Virus (EBV): [more info]
- 670 Azadirachta indica {Neem}
- Neem (Azadirachta indica) demonstrates notable antiviral activity against Epstein-Barr Virus (EBV) and other herpes-type viruses: [more info]
- 611 allium sativum {garlic}
- Garlic (Allium sativum) and its organosulfur compounds (OSCs) exhibit notable antiviral activity against Epstein-Barr Virus (EBV) in preclinical studies: [more info]
- 747 Olea europaea {Olive leaf}
- Amino Acid and similar
- 515 –(2S)-2-amino-5-carbamimidamidopentanoic acid {arginine}
- Inhibition of EBV reactivation via nitric oxide (NO): Supplementation with L-arginine in EBV-positive cell cultures inhibits spontaneous EBV reactivation. [more info]
- 378 a-Amino-3-indolepropionic acid {Tryptophan}
- EBV and tryptophan depletion: EBV infection induces the enzyme indoleamine 2,3-dioxygenase (IDO) in immune and tumor cells, which degrades tryptophan into kynurenine. [More info]
- 515 –(2S)-2-amino-5-carbamimidamidopentanoic acid {arginine}
At this point, I will leave reviewing other items on the consensus report to the reader.
Bottom Line
I must confess, this post blew me away — we got key bacteria identification from just 5 annotated samples – still uneasy about that. The number of bacteria shifted was huge with key suggestions being items known to be effective for treating EBV.
I think we have enough to set a course of action. I would suggest trying for 2 months (one probiotic cycle) and then doing a retest. If finances can afford it, repeat Thorne (to allow comparisons) and also do a Biomesight test (to allow taxa filtering by symptoms).
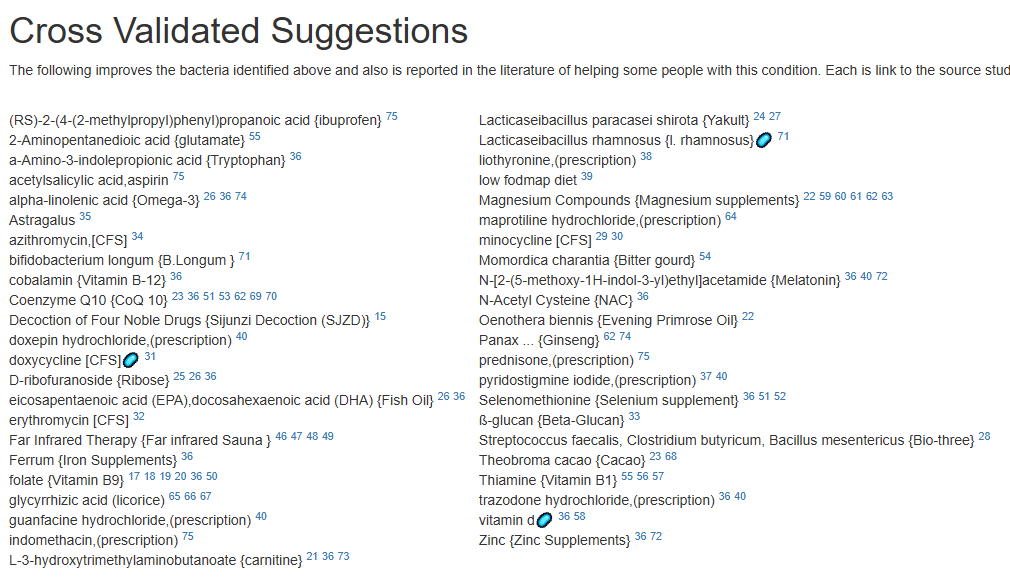
For a list of more documented items that help EBV infections, see Treatment of Epstein-Barr virus (EBV) in ME/CFS Context
Questions From Reader
Thanks, Ken. That is a lot of information to take in. I’ll try to summarize my takeaways and questions:
- – Transfer factor: How did your wife receive the EBV-specific? Was it through a medical facility, or did it used to be available as a supplement? .. Does not seem like there is much actionable for me to do on this other than consider trying one of the non-specific bovine supplements.
- It was available for order on the internet from a company in the eastern US. I recall it was mare( female horse) based. Thus likely high overheads and then the FDA became concern about transfer of other infections. Sterilization of the Transfer Factor likely killed it.
- – Coagulation: Hemex panel no longer available. The Dedimed lab in the linked post appears it might be closed. (website down, last social media post was in 2023) .. Aware of any alternatives?
- I am sorry to see that it is gone. It means that you may have to fight with the specialists for each test done. I asked perplexity on best DNA test
“Blueprint Genetics provides the most comprehensive DNA testing for inherited coagulation factors among the providers in the search results. Their Bleeding Disorder/Coagulopathy Panel covers 71 genes, including all major and many rare genes associated with inherited bleeding and coagulation disorders. This panel assesses both coding and non-coding variants, which increases the likelihood of detecting clinically relevant mutations”. [More Info]
Site: https://blueprintgenetics.com/
- I am sorry to see that it is gone. It means that you may have to fight with the specialists for each test done. I asked perplexity on best DNA test
- – I have read of your aspirin experiment – not sure I am that brave. I am considering trying with some combination of Bromelain, Natto, Lumbro, Serra, Bosweilla, etc. … Based on your fibrinolytics and half-life posts. Thoughts on a strategy?
- Conceptually it’s good. A reasonable shot in the dark. This page shows the coagulation cascade. One or more of the arrows shown below may be defective. Each of these substances affects one or more of the arrows. Watch out for “overdoing” some part of the cascade and you became an easy bleeder and the bleeding takes a long time to end.

– Probiotics: I’m struggling a bit here trying to combine the lists from two sections in the article to get a 2-month rotation:
What should be #3? Still a “mixture of Baccillus” or one of the single strains below
- 841 — Enterococcus faecium [EBV] — Recommended to increase by both methods #1 (2weeks)
- 676 — Lactococcus cremoris —
- 468 — Bifidobacterium adolescentis – 206
- 422 — Akkermansia muciniphila [EBV] – 265 – Recommended to increase by both methods #2 (2weeks)
- 350 — Lactococcus lactis [EBV] – 30 – Recommended to increase by both methods
- 190 — Bifidobacterium breve {B. breve} – 226 — Decreases the Corynebacterium #4 (2weeks)
- 205 — Levilactobacillus brevis – 512
- 95 — Ligilactobacillus salivarius {L. salivarius} – 30
- 291 — Bifidobacterium catenulatum – 154
- Quick start (focus on solution): Take the following 3 concurrently for a month. Usually I tend to go slow with one at a time, but I am interested if they will “kick ass”. Given that onset is so recent compare to most people, a targeted jump start is worth the experiment.
- * Enterococcus faecium https://www.ebay.com/itm/325338234904?_skw=enterococcus+faecium
- Akkermansia muciniphila https://pendulumlife.com/products/pendulum-akkermansia
- Lactobacillus casei Shirota (Yakult) Most Groceries stores!
– After 2 months retest with both Thorne and Biomesight – Yes, Biomesight allows you to use discovered associations and thus focus solely on the (likely) causal bacteria. Thorne to allow comparison of changes.
– Vitamins: – Understood. Already doing most of these. – Double check the to Avoid List, often people forget that step.
– Diet: – My high level takeaway from trying to use the tools on the report was “high fiber, less fat.” But that was just based on the “just tell me what to take or avoid” with no attempt to nuance for EBV. Not sure how to do that?
Good question: no attempt to nuance for EBV. Not sure how to do that? — classic issue of sparse data,,,, I asked Perplexity and got https://www.perplexity.ai/search/are-there-any-diet-changes-fou-psucBMISRi2DEBw_.VFddA#0 Most appear to be based on speculation… This is the best of the citations: https://journals.sagepub.com/doi/10.1177/2150131915573472 “However, after adjusting for potential confounders the results for both dietary factors and food insecurity were no longer statistically significant. ” so no data to work from.. 🙁
Thanks again for the effort you’ve put into this already. I’m quite amazed at how quickly you’ve put it together.
Postscript and Reminder
As a statistician with relevant degrees and professional memberships, I present data and statistical models for evaluation by medical professionals. I am not a licensed medical practitioner and must adhere to strict laws regarding the appearance of practicing medicine. My work focuses on academic models and scientific language, particularly statistics. I cannot provide direct medical advice or tell individuals what to take or avoid. My analyses aim to inform about items that statistically show better odds of improving the microbiome. All suggestions should be reviewed by a qualified medical professional before implementation. The information provided describes my logic and thinking and is not intended as personal medical advice. Always consult with your knowledgeable healthcare provider.
Implementation Strategies
- Rotate bacteria inhibitors (antibiotics, herbs, probiotics) every 1-2 weeks
- Some herbs/spices are compatible with probiotics (e.g., Wormwood with Bifidobacteria)
- Verify dosages against reliable sources or research studies, not commercial product labels. This Dosages page may help.
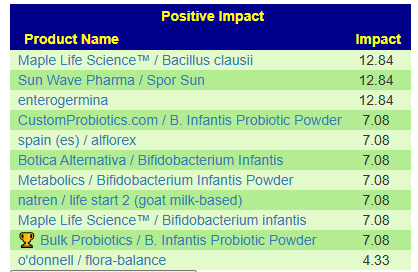
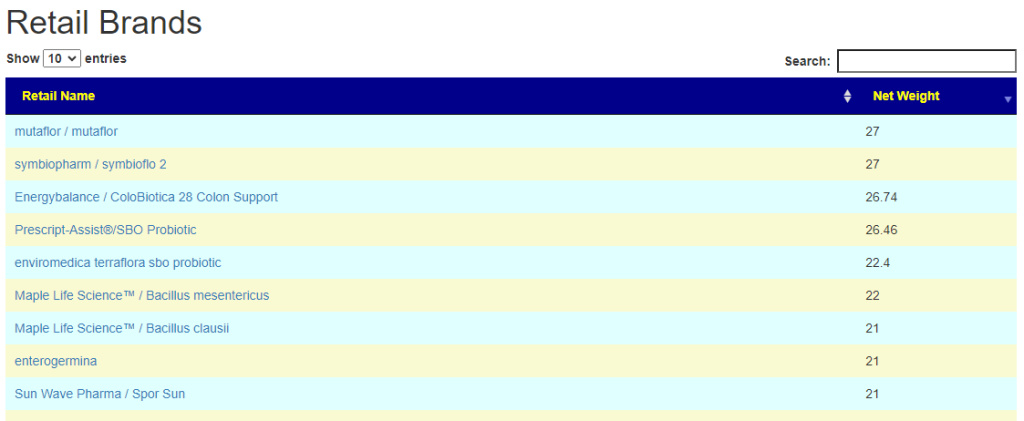
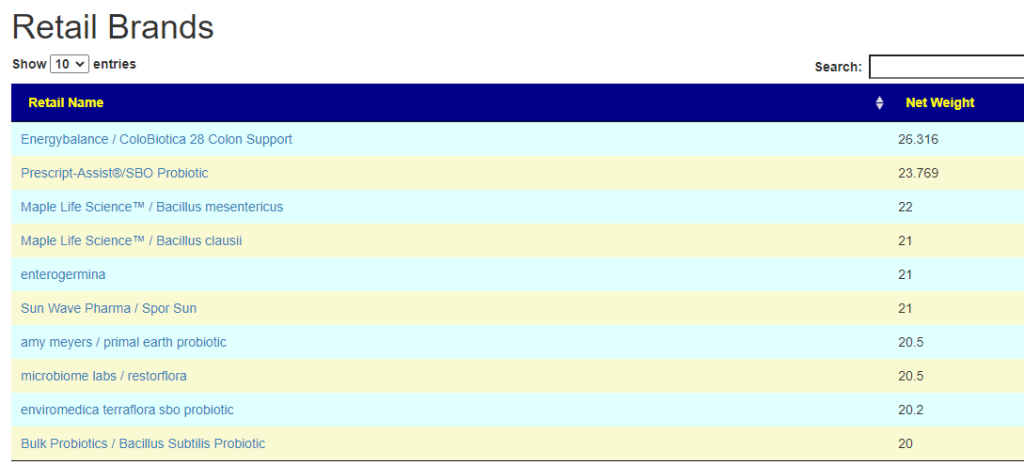
- There are 3 suppliers of probiotics that I prefer: Custom Probiotics , Maple Life Science™, Bulk Probiotics: see Probiotics post for why






















Recent Comments